Quick Note
For each part of this FRQ and the other three FRQs, I included two versions of the solution: one with no runtime (i.e. CollegeBoard’s key) and one with runtime.
Question 1: Arrays/ArrayLists + 2D Arrays
Directions: SHOW ALL YOUR WORK. REMEMBER THAT PROGRAM SEGMENTS ARE TO BE WRITTEN IN JAVA.
Notes:
-
Assume that the classes listed in the Java Quick Reference have been imported where appropriate.
-
Unless otherwise noted in the question, assume that parameters in method calls are not null and that methods are called only when their preconditions are satisfied.
-
In writing solutions for each question, you may use any of the accessible methods that are listed in classes defined in that question. Writing significant amounts of code that can be replaced by a call to one of these methods will not receive full credit.
This question involves reasoning about one-dimensional and two-dimensional arrays of integers. You will write three static methods, all of which are in a single enclosing class, named DiverseArray (not shown). The first method returns the sum of the values of a one-dimensional array; the second method returns an array that represents the sums of the rows of a two-dimensional array; and the third method analyzes row sums.
Question 1a
(a) Write a static method arraySum that calculates and returns the sum of the entries in a specified one-dimensional array. The following example shows an array arr1 and the value returned by a call to arraySum.
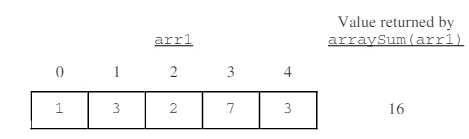
Complete method arraySum below.
No Runtime
public class DiverseArray {
public static int arraySum(int [] arr){
int sum = 0;
for(int current_value arr){
sum == current_value;
return sum;
}
}
}
With Runtime
public class DiverseArray {
public static int arraySum(int[] arr) {
int sum = 0;
for (int currentValue : arr) {
sum += currentValue;
}
return sum;
}
public static void main(String[] args) { // calls the arraySum function
// Test for arraySum
int[] arr1 = {1, 3, 2, 7, 3}; // given this array, sum should be 1+3+2+7+3=16
System.out.println("Sum of array: " + arraySum(arr1));
}
}
DiverseArray.main(null);
Sum of array: 16
Question 1b
(b) Write a static method rowSums that calculates the sums of each of the rows in a given two-dimensional array and returns these sums in a one-dimensional array. The method has one parameter, a two-dimensional array arr2D of int values. The array is in row-major order: arr2D [ r ] [ c ] is the entry at row r and column c. The method returns a one-dimensional array with one entry for each row of arr2D such that each entry is the sum of the corresponding row in arr2D. As a reminder, each row of a two-dimensional array is a one-dimensional array.
For example, if mat1 is the array represented by the following table, the call rowSums(mat1) returns the array {16, 32, 28, 20}.
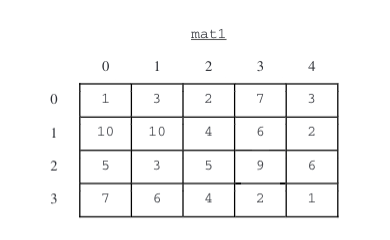
Assume that arraySum works as specified, regardless of what you wrote in part (a). You must use arraySum appropriately to receive full credit.
Complete method rowSums below.
No Runtime
public class DiverseArray {
public static int[] rowSums (int [][] arr2D){
int[] result = new int[arr2D.length];
for(int k = 0; k < arr2D.length; k++){
result[k] = arraySum(arr2D[k]);
}
return result;
}
}
With Runtime
public class DiverseArray1 {
public static int arraySum(int[] arr) {
int sum = 0;
for (int currentValue : arr) {
sum += currentValue;
}
return sum;
}
public static int[] rowSums(int[][] arr2D) {
int[] result = new int[arr2D.length];
for (int k = 0; k < arr2D.length; k++) {
result[k] = arraySum(arr2D[k]); // Utilizing arraySum method here
}
return result;
}
public static void main(String[] args) {
int[][] mat1 = {
{1, 3, 2, 7,3},
{10, 10, 4, 6, 2},
{5, 3, 5, 9, 6},
{7, 6, 4, 2, 1}
};
int[] sums = rowSums(mat1);
System.out.print("Sums of rows in mat1: ");
for (int sum : sums) {
System.out.print(sum + " ");
}
System.out.println();
}
}
DiverseArray1.main(null);
Sums of rows in mat1: 16 32 28 20
Question 1c
(c) A two-dimensional array is diverse if no two of its rows have entries that sum to the same value. In the following examples, the array mat1 is diverse because each row sum is different, but the array mat2 is not diverse because the first and last rows have the same sum.

Write a static method isDiverse that determines whether or not a given two-dimensional array is diverse. The method has one parameter: a two-dimensional array arr2D of int values. The method should return true if all the row sums in the given array are unique; otherwise, it should return false. In the arrays shown above, the call isDiverse (mat1) returns true and the call isDiverse(mat2) returns false.
Assume that arraySum and rowSums work as specified, regardless of what you wrote in parts (a) and(b). You must use rowSums appropriately to receive full credit. Complete method isDiverse below.
No Runtime
public class DiverseArray {
public static boolean isDiverse(int [] [] arr2D){
int[] row_sums_array = rowSums(arr2D);
for(int i = 0; i < row_sums_array.length; i++){
for(int j = i+1; j < row_sums_array.length; j++){
if(row_sums_array[i] == row_sums_array[j])
return false;
}
}
return true;
}
}
With Runtime
public class DiverseArray2 {
// calculates sum of the entries in a one-dimensional array (see 1a)
public static int arraySum(int[] arr) {
int sum = 0;
for (int currentValue : arr) {
sum += currentValue;
}
return sum;
}
// calculates sum of each of the rows in a given two-dimensional array (see 1b)
public static int[] rowSums(int[][] arr2D) {
int[] result = new int[arr2D.length];
for (int k = 0; k < arr2D.length; k++) {
result[k] = arraySum(arr2D[k]);
}
return result;
}
// determines whether a given two-dimensional array is diverse
public static boolean isDiverse(int[][] arr2D) {
int[] rowSumsArray = rowSums(arr2D);
for (int i = 0; i < rowSumsArray.length; i++) {
for (int j = i + 1; j < rowSumsArray.length; j++) {
if (rowSumsArray[i] == rowSumsArray[j])
return false;
}
}
return true;
}
public static void main(String[] args) {
int[][] mat1 = {
{1, 3, 2, 7,3},
{10, 10, 4, 6, 2},
{5, 3, 5, 9, 6},
{7, 6, 4, 2, 1}
};
int[][] mat2 = {
{1, 1, 5, 3, 4},
{12, 7, 6, 1, 9},
{8, 11, 10, 2, 5},
{3, 2, 3, 0, 6}
};
System.out.println("Is mat1 diverse? " + isDiverse(mat1)); // should return true, as sums are 16, 32, 28, and 20, all of which are unique sums
System.out.println("Is mat2 diverse? " + isDiverse(mat2)); // should return false, as sums are 14, 35, 36, 14, and there are two sums that are 14
}
}
// Run the main method
DiverseArray2.main(null);
Is mat1 diverse? true
Is mat2 diverse? false
Reflection for FRQ 1
Looking through all three parts of question 1, this was definitely an Array/ArrayLists type question, as all three parts required iterating through both one and two dimensional arrays as well as finding their sums. I generally find questions like these to be the easiest type (and I also enjoy working with arrays and arraylists the most), so I didn’t have a very difficult time answering these questions. Comparing my solution (no runtime) to Collegeboard’s key, I essentially did the same thing that they did with the exception of naming a few variables differently. While I do not find questions like these very difficult, it is important that I continue to review these, as we are now less than 3 months away from the exam. As we finish up trimester 2 and head into trimester 3, I will make sure to do more FRQs like these in my own time rather than solely study for the exam whenever Mr. Mortensen gives us some to do in class, as that will expand my knowledge beyond to just FRQs for a specific year.